The H2 Wiki

demystifying-dlist

Demystifying DList

Introduction

You may have heard that repeated left-associated appends on linked lists are slow. You may also have heard that the “difference list”, implemented in Haskell as “DList”, makes left-associated appends reasonable. The type of DList is somewhat mysterious. What’s really going on? In this article I will explain with nice diagrams.

The problem with lists

Suppose I append some lists using (++) in some arbitrary fashion. What evaluations are performed as we pattern match on the result, pulling off the head? I’ll show you an example Haskell expression, and then a graphical representation to explain the resulting computation. The expression is

(((as ++ bs) ++ (cs ++ ds)) ++ (es ++ (fs ++ gs)))

and the tree structure that arises in memory is this

In-memory structure of appends

What happens when we pattern match this? Well, the definition of append is

xs ++ ys = case xs of []      -> ys
                      (x:xs') -> x : (xs' ++ ys)

so we walk down the left branch of the first (++) node and pattern match the child node. However, the child node is itself a (++) node, so we again walk down the left branch and pattern match the grandchild. We have to keep walking down the left branches until we reach an already-evaluated list cell, in this case as. Then if as is a cons a:as' we replace as with as' and float the a back to the top. Thus it has taken \(O(d)\) operations to pattern match our structure, where \(d\) is number of left branches from the root to the leaf containing as.

If we keep pattern matching on the result, continuing to pull off the head of each resulting tail, then we perform \(O(d)\) operations each time we pull off the next element of as. Retrieving all of as thus takes \(O(dn)\) operations, where \(n\) is the length of \(as\).

Once all of as has been floated up to the top, the (++) node is replaced by bs and we start matching bs, now walking \(d-1\) steps down the tree to retrieve each element.

In general, it seems that to retrieve a single element from a list ls in the append expression takes \(O(l)\) operations where \(l\) is the number of left branches you have to traverse to reach the leaf containing ls. Left branches correspond to left-associated appends, so this is why left-associated appends are problematic.

However, contrary to popular belief, it seems that the list as is not walked several times in the construction of the result. This belief may be a hangover from those who are more familiar with the behaviour of strict languages.

Improving performance

Once upon a time some clever person noticed that if you encode a list as the action of preappending it then this bad left-associated append behaviour goes away.

(The earliest reference I can find is John Hughes, A Novel Representation of Lists and its Application to the Function “Reverse”. The technique seems well known in the Prolog community, too.)

The encoding can be done, for example, as

type DList a = [a] -> [a]

fromList :: [a] -> DList a
fromList xs = (xs ++)

toList :: DList a -> [a]
toList xsf = xsf []

append :: DList a -> DList a -> DList a
append xsf ysf = xsf . ysf

Notice that

toList (fromList xs `append` fromList ys)
         = ((xs ++) . (ys ++)) []
         = xs ++ ys ++ []
         = xs ++ ys

so indeed we have a decent encoding of lists. But what does this gain us?

Let’s observe what computation occurs when we take the head of a DList. We’ll use the same list append calculation as before, but encoded into DList form. It looks complicated as an expression, but nice as a tree.

((((as++) . (bs++)) . ((cs++) . (ds++))) . ((es++) . ((fs++) . (gs++))))

This is a function, and converting it to a list is done by applying the function to []. The resulting structure is depicted here.

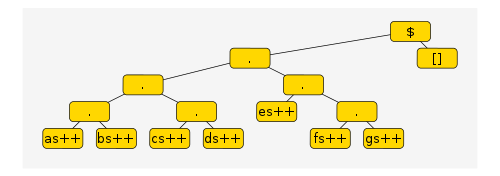
Stage 1

What happens when we pattern match this? We have a computation of the form f . g $ x, which evaluates to f $ g $ x. If f itself is a composition, the computation repeats the same evaluation step on f. At each stage if the outermost function call is a composition, the composition is unwound to a function application. This proceeds until the outermost function call is something that can pattern matched directly, i.e. (as ++), the leftmost list in our append expression.

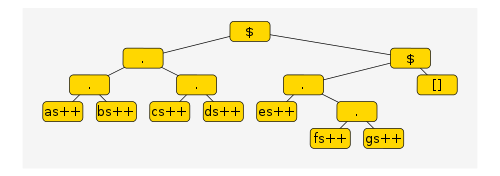
Stage 2
Stage 3
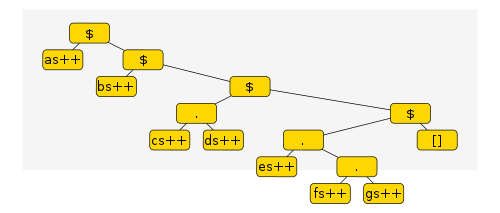
Stage 4

Why is this better?

Now after performing \(O(d)\) operations the computation has reached a state where we can pull out all of as in one go. Retrieving all of as is then \(O(d + n)\) rather than \(O(dn)\). An excellent reduction! Furthermore, it looks like every left branch only has to be transformed once no matter how many leaves that branch supports, so the total cost of reading through the whole list is \(O(D + N)\) where \(D\) is the number of left branches and \(N\) the sum of the lengths of each leaf.

Why did we need functions?

Having observed the mechanism behind the DList algorithm, we can ask ourselves “Why is it encoded with functions?”. After all, the algorithm itself is simple, but the implementation piggybacks on Haskell’s function evaluation procedure in an opaque manner, perhaps unnecessarily. For example, one could also encode the algorithm like this

data Tree a = Leaf a | Branch (Tree a) (Tree a)

fromList :: [a] -> Tree [a]
fromList = Leaf

toList :: Tree [a] -> [a]
toList (Leaf x) = x
toList (Branch (Leaf x) r) = x ++ toList r
toList (Branch (Branch l1 l2) r)
               = toList (Branch l1 (Branch l2 r))

append :: Tree [a] -> Tree [a] -> Tree [a]
append = Branch

The toList defined here in terms of a binary Tree datatype performs exactly the same algorithm as the DList but without mysteriously hiding it behind function calls and piggybacking on Haskell’s evaluation procedure.

In practice it is indeed much faster than naive append. If you like you can try the following:

foldlTree = length (toList (foldl Branch (Leaf []) (map (Leaf . return) [1..20000])))

foldlList = length (foldl (++) [] (map return [1..20000]))

I don’t know if DList will be faster than the Tree approach for some reason. I haven’t benchmarked.

Generalizing

The DList concept generalizes to the “codensity transformation” which makes left-associated monadic binds more efficient. The codensity transformation was first outlined, I believe, by Janis Voigtlander. It’s not clear to me, though, whether the Tree datastructure generalizes equivalently.

Conclusion

It’s simple to understand how the DList algorithm works once you demystify its use of function composition. However, it’s not clear if the more concrete implementation using Tree generalizes as well as the DList method.

References